Editor's Note: This is a continuation of the article Is Your Favorite Sport Choosing The Best Team Fairly?. I suggest reading at least the first part of it for context.
Growing up in Georgia, I was a fan of the Atlanta Braves and Falcons. Being a fan of the Braves in the '90s and early 2000s was both fun and emotionally traumatic. From 1991 to 2005, the Braves won an unprecedented 14 straight NL East division pennants, appeared in the world series 5 times...and only won once.
How could a team dominant enough to win 14 straight division titles only come away with one world series victory? As it turns out, the fault may not have been with the team, but with the system.
Baseball Isn't Exactly Fair
Let's just start off by acknowledging that baseball is a weird game. Every ballpark has a different size outfield and half the teams in the league have a different rule (designated hitter) than the other half! It's enough to make OCD sports fans such as myself go completely insane. It's a game steeped in tradition, so changing it has proved difficult over the years. Remember though, just because you've always done it doesn't mean it's not incredibly stupid.
It's also a game where a hitter can fail two out of three times and be considered "great". Likewise, a great pitcher can throw 99 fantastic pitches that batters can't even touch, but if he hangs just one right in a batter's sweet spot, then it could be home run city. This isn't the end of the world, but in close games it could mean the difference. Meanwhile, the pitcher for the other team could be all over the place, but if a team's batter's can't take advantage then it doesn't do them much good.
In short, baseball is a very statistical game. In the major leagues, being "good" at baseball is kind of like being "good" at blackjack. Yes, it is possible through solid skills and strategy to win, but you are merely giving yourself a slight statistical advantage, you're not guaranteeing victory.
The thing with slight statistical advantages is that they rely on a large sample size to manifest themselves. If you are good at blackjack, then you have to be prepared to sit at a table for many hands (and possibly lose a fair amount of money) before you can expect to start making money.
I'll spend the rest of this article explaining the research I did on the past 25 seasons of Major League Baseball and some of the conclusions I've come to based on probabilistic analysis. Let me just say that before I started this, I had a slight hunch that World Series winners probably weren't always the best teams, but now I just have absolutely no faith in the system whatsoever.
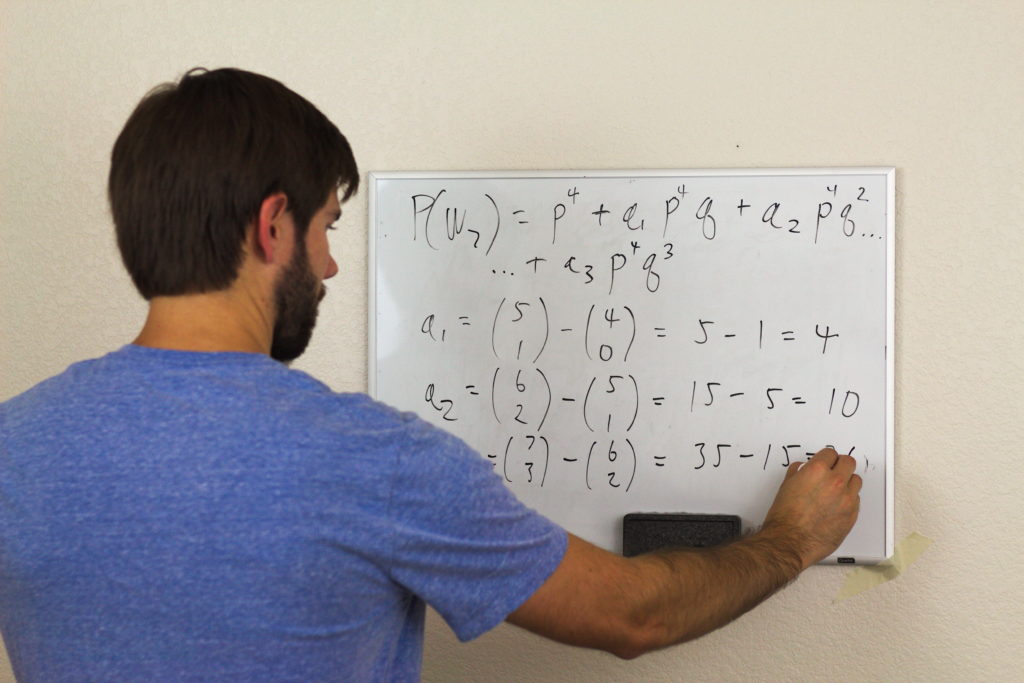
Parents: talk to your nerdy kids about ruining sports with math. If we all work together, we can end it in our lifetime
How Baseball Determines a Champion
Compared to other sports, baseball has a pretty long regular season. This was done on purpose, because people realized that baseball is a very statistical game and needs a large sample size, i.e. number of games, for any team to prove their worth. For that reason, the baseball seasons lasts for 162 games.
And you know what, that's probably a decent enough number. The season lasts from early April to early October, gives everyone something to do for the summer, and is over just in time for football to start (because once football starts, who really cares about baseball anymore?).
So after 162 games there should probably be one team that is better than the rest, so we should just crown them as the champion right? Haha, nope.
Instead, the current system makes a playoff with the division winners from three divisions in each league (again, friggin arbitrary divisions and leagues are the bane of American sports) and two wild card teams (the wild cards duke it out in a single game playoff...which is a terrible idea as you will see). The playoff is eight teams in total (after the wild card game) and consists of three rounds, the first a best-of-five series and the second two are a best-of-seven series.
"But Zach," you say, "doesn't having the multi-game series format allow for the better team to prevail in the long run?"
You can't see it, but I'm smugly laughing at you right now.
What Are the Chances?
For this study, I've assumed a simple probabilistic equation for predicting winners of a game. For teams A and B that each have known probabilities of winning any single game, the probability that Team A beats Team B is equal to:
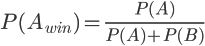
Where P(A) and P(B) are the respective probabilities that Team A and Team B will win any game. These are impossible to determine exactly, given the many random variables present in sports, but one can use a team's overall record to give a decent estimate for their likeliness of winning any game. The more games they have played, the more accurate this becomes.
Win Data from 1990-2015
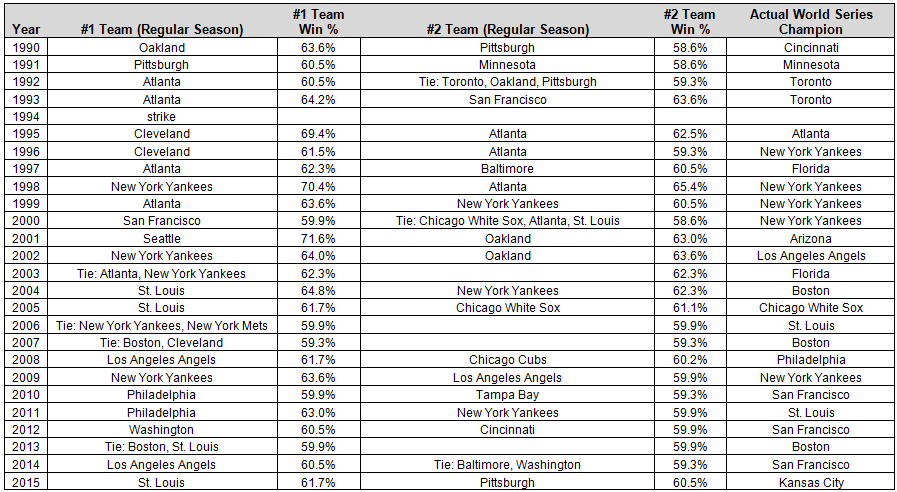
To put some real numbers with this, I analyzed the data from the past 25 MLB seasons to see who the two teams with the best regular season records were. The teams and their records are shown below, along with the actual World Series champions.
We can see a few things from this data. One, that the records between the #1 and #2 teams often do not differ by much, and two, that the team with the best regular season record won the world series a mere 4 times out of 25 seasons, for a winning percentage of 16%. To put that in perspective, the probability of picking playoff series champions at random is 14.5% (accounting for there only being a 4 team playoff in the 1990-1993 seasons).
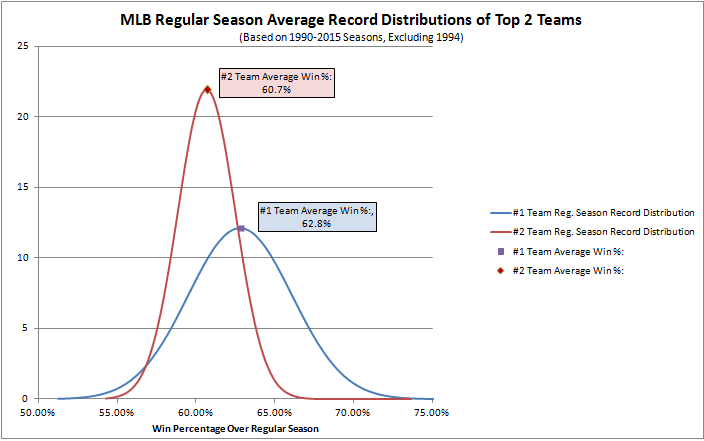
Here I have plotted the Gaussian distributions of the top 2 regular season teams averaged over the past 25 seasons:
If you are unfamiliar with Gaussian (Normal) distributions, then you should have paid more attention in your college statistics class. If you weren't required to take a statistics class in college, then you went to the wrong college.
Basically, the above plot is determined based on the average and standard deviation of the #1 and #2 teams in the regular season, which seeks to infer what the chance is that a #1 team is actually better than a #2 team.
Where the plots intersect means that the #1 vs. #2 team is fairly ambiguous, i.e. a team with a winning percentage between ~57% and ~63% could be the best, but they could also equally likely be the second best. If your winning percentage is above 65%, then there is a really good chance that you are the undisputed best team in the league.
It's surprising then, that the team with the best overall record in baseball in the past 25 years, the 2001 Seattle Mariners, with a winning percentage of 71.6%, didn't even make it to the World Series. Well, is it surprising? Perhaps not, as you will see.
In a playoff series, teams will be pitted against the other top teams in the league, which means that their chance of winning will probably be less than that of the regular season. If we put the average #1 and #2 team winning percentages into the win prediction formula, then the resultant probability that the #1 team will beat the #2 team in a single game is a whopping 50.85%. That's a whole 0.85% better than chance.
So, basically, we could save everyone a lot of time by just deciding the world series champions with a coin toss.
Doesn't Playing a Best-of-Seven Game Series Improve the Odds of the Better Team Winning?
Yes, it does, but not by much.
In order to compute the probability that a team will win a best-of-N game series, you have to figure out the probabilities of each particular scenario that allows them to win, i.e. the chance that they win in the minimum number of games, the minimum plus one, etc.
For a best-of-seven game series, the probability that a team will win is given as:
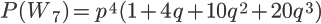
Where p is the probability that they win a single game and q is the probability that they lose a single game.
If you plug the average win prediction of 50.85% into the above formula, then you'll find that the "top" team will win the series...wait for it...51.86% of the time! Yay! By playing a best of seven game series we've increased the better team's chance of winning by a whole percent! That should make it pretty obvious who the better team is!
This, of course, brings up the question: what if we played more games? I too wondered this, and had to figure out a general formula for the win probability of a best-of-N game series (it's tricky because increasing N has the effect of adding higher order terms to the polynomial, making it hard to write something in Excel).
Instead of programming an iterative loop to compute the probability, I just did a massive table in Excel that goes up to a best-of-163 game series (since the regular season is 162 games). In case you are interested, the multipliers of the 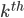 order q terms are:
order q terms are:
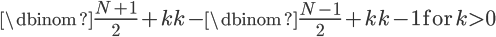
So, for a best-of-163 game series, assuming an average win probability of 50.85% for our team, they will win the series about 58.61% of the time.Remember, that's just the probability that they win one series, much less the entire 3 round playoff.
Let's explore a real life scenario and assume that we are the 2001 Seattle Mariners, the team with the best regular season record in baseball over the past 25 years. We have made it to the playoffs and get a top seed in the AL. Our first opponent is the Cleveland Indians (or is it Native Americans?), with a record of 0.562. Our probability of beating Cleveland in a single game is 56.03%, and our probability of beating them in a best-of-5 game series is 61.19%. It's not great, but it's a tad better than a coin flip.
Let's say we win the series (which they did in real life). Our next opponent is the New York Yankees, with a record of 0.594. Our chance of beating them in a single game is 54.66%, and our chance of beating them in a best-of-seven game series is 60.1%. Let's say we win this series as well (in real life they lost 4-1), so our opponent in the world series is the Arizona Diamondbacks, with a record of 0.568 (who won the world series in real life). Our chance of beating them in a single game is 55.76%, and our chance of beating them in a best-of-seven game series is 62.44%.
To determine what Seattle's overall probability of winning the world series is, we must multiply the probabilities that they win each playoff series together. This equates to 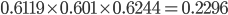 . So, the best team in baseball, with a regular season record in a pretty statistically significant area of the bell curve has a 22.96% chance of winning the world series. It's better than pure chance...by 10.5%. Still, it's worse than the odds of correctly calling a coin toss two times in a row.
. So, the best team in baseball, with a regular season record in a pretty statistically significant area of the bell curve has a 22.96% chance of winning the world series. It's better than pure chance...by 10.5%. Still, it's worse than the odds of correctly calling a coin toss two times in a row.

Yay! We got lucky!
Image Credit
Other Reasons Not to Have a Playoff
Numbers aside, I think a bigger reason that a playoff series doesn't make sense in baseball is that, psychologically, it breaks from the norm. In baseball, the large number of regular season games means that each game is equally insignificant. Teams celebrate wins with high fives and mourn losses with "aw shucks, better luck next time." This dynamic changes completely in the postseason, when all of the sudden every game matters. For the players, I can only imagine that this is a difficult mental transition to make.
The atmosphere changes as well. Instead of playing in front of a boozy crowd who decided to spend a lazy summer evening at the ballpark, teams are playing in front of an amped up group of sports fanatics who desperately want to see their team win the World Series. Further, baseball is supposed to be a summer sport, and because the postseason usually starts in October and lasts until early November (when many American cities start to get pretty chilly), teams are forced to play in weather conditions that they haven't had to play in the entire season.
While the playoff may be more or less chance, there have been some franchises, notably the New York Yankees, that have achieved considerable World Series success. The Yankees have appeared in 40 World Series and won 27, for a percentage of 67.5%. This is, as you can see, better than pure chance, although not considerably.
One thing the Yankees have going for them is that they are an old franchise, so they have had the opportunity to win many World Series titles. And yes, many of the Yankees teams of the past probably were really good, as pre-1969 you had to be the best team in the AL or NL to make it to the World Series (it was only a one-round playoff). This made things actually more fair, as the best regular season team had at least a 50/50 shot of winning the World Series, instead of having to endure 3 rounds of playoffs.
The other, and possibly more important thing, that the Yankees have going for them is that they have a rich history of winning. I have a personal theory (that has been empirically proven in my tennis matches) that winning is a positive feedback loop, i.e. the more you win, the more confidence you gain, and the more likely you are to win in the future.
In my brute force vs. precision article I talk about how precision athletes are more likely to have poor performances when the stakes are high. In baseball, pitching is a very precision activity, and something that a team must do well if they hope to win. So let's take, I don't know, the 2001 Seattle Mariners (a franchise that has never even been to a World Series) and pit them against, I don't know, the New York Yankees (a team that has won 27 World Series titles). On one hand, you have a team that had an amazing regular season, and is probably imagining that they will be the heroes who finally bring their city its first World Series title. One the other hand, you have a team who won the World Series the past three years.
Who do you think is going to feel more pressure? The team with a rich history of winning World Series titles, or the team who has never even been before and probably is thinking that this is their best shot at doing so. In tight situations, it's these little things that can skew the odds in favor of the team with a richer history of winning. This is, of course, prevalent in all sports, but seeing as how in baseball the odds of a team winning in the playoffs are more or less a toss up, it's pretty significant.
What's the Solution?
Basically, the best way I can see this going down is to quit it with the stupid leagues and divisions altogether and just have a sextuple round robin between every team in the league, consisting of a 174 game regular season (just 12 more than it is now) and NO PLAYOFF. Each team plays a 3 game series at home and a 3 game series away with every other team. That's it, just pick the team at the end with the best record and be done with it. What if 2+ teams tie? Figure out a tiebreaker. What about the World Series? Just don't have one.
Is this perfect? No. Could there be two or more teams at the end who don't have statistically significant enough record differences to confidently crown one the champion? Sure. But there is just no way to have a baseball playoff in a reasonable number of games that decides things any better than a coin flip.
Will this ever happen? Probably not, seeing as how things seem to be going the opposite way since they keep adding more teams to the playoffs.
So, unfortunately, baseball fans will just have to live with the fact that the World Series champion isn't necessarily the best team, just the team that happened to win the World Series. Oh, and a Harvard study agrees with me on this. They used the Pythagorean win expectation formula to compute their results, but we came to more or less the same conclusion.
Shout Out to My Braves
Based on pure regular season win percentages, the Atlanta Braves should have appeared in the World Series 8 times between between 1992 and 2003, and should have won 4.5 times (they tied with the Yankees one year). The fact that they didn't win is not their fault, it's a messed up system that they were on the business end of.
So rest easy, '90s Braves, you truly were the best, don't let anyone tell you differently.



Pingback: Is Your Favorite Sport Choosing the Best Team Fairly?
Pingback: Why Nerds Love to Head Bang: A Primer on Prog Metal