When I was in college thinking about what senior electives to take, I recall professors saying "you don't want to be a mile wide and an inch deep, but you also don't want to be an inch wide and a mile deep."

The message was pretty clear: don't make yourself too well-rounded because you won't have any real useful abilities in any particular area. It was also a warning against focusing on one specific thing for all your studies, because then that would be the only thing you are good at.

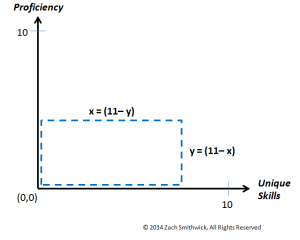
To further reiterate this point, let's do a little geometry lesson. Let's assume, just to make the math easy, that the x-axis of a rectangle represents your different, unique, skill sets. The y-axis, on the other hand, represents your proficiency in a particular area. To be somewhat realistic, let's say that each axis can only go to a maximum of 10, and the other axis varies as 11 - [other axis value]. So, if you wanted to be a 10 in proficiency at something, then you would only be able to be a 1 in unique skill set (going along with the inch wide, mile deep analogy).

Okay, so let's also assume for the sake of this analogy that the area of the rectangle represents your complete skill level, and that is what you are trying to maximize. So, the area would be equal to x*(11-x) or equivalently y*(11-y), since you choose the value for one side and then calculate the length of the other side based on that.

So, the question becomes: how do you get the maximum skill level (area of rectangle) ?

Well, it's pretty simple to calculate. Let's set the area as a function of x, so A(x) = x*(11-x), or equivalently A(x) = -x^2 + 11*x (using the distributive property). Now, brush up on your differential calculus by taking the first derivative of A(x).

So, A'(x) = -2*x + 11. To find the maximum area, set the derivative equal to zero, or A'(x) = 0.
Finally, 0 = -2*x + 11, solving for x gives 2*x = 11, x = 5.5.

A-ha! We've found that 5.5 is the optimal x value to maximize the area of the rectangle! What does that give for y?
y = 11 - x => y = 11 - 5.5 = 5.5!

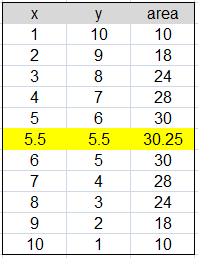
So, the maximum area is a square with sides equal to 5.5! This is a handy little thing to know: if you have a rectangle and are trying to maximize area, and one side varies opposite the other side, then the maximum area will be a square. Don't believe me? Plug several numbers into the equation for area and see what the results are. Too lazy? Fine, I'll do it for you.

You can see that the 5.5 square gives the highest area, and that each side (maximizing x or y) is symmetrical. So why did we have to do calculus to talk about life skills? Because now you know that it isn't good to be good at only one thing, and likewise not good to be good at a bunch of different things.

Sure, this is just a rough mathematical approximation to something very complex, but you can see how it holds a certain amount of truth. With things like time management and maybe a touch of brilliance, you could conceivably become very skilled at a vast array of things without compromising depth, but for most of us skill in some areas involves neglecting other things.

I think this is a good place to start, but not exactly what I would recommend. Using this model, it would imply that you can become 55% as skilled as you could be in 55% of the things in which you would like to be skilled. Now, that's a little over half, which isn't bad, but also not particularly useful if you ask me.

For most people, you want to get a job, or better yet, a career, doing something in order to make money. If you want that career to pay well, then you should probably be good at it. In order to be good at it, then you will probably have to use more than 55% of your total abilities for it. So that's a tad of a downer, but it doesn't have to be.

All it means is that you might have to compromise a few of your other skills in order to develop one "big" skill. But here's the thing: don't compromise the other skills so much that they are completely useless. In an industrialized society, it is common to put all your eggs in the "career skills" basket and leave everything else alone. This makes the most logical sense for a society, but if you look at the chart above then you can see how this gives the worst individual performance (an area of 10 as opposed to 30.25) !  The problem is that you have an entire population of people who are really good at only one thing and know very little about other things. If you know very little about other things, then it will make it harder to predict problems that could happen in other areas affected by your career. You see, nothing really happens in a vacuum. Your career may be specific, but it will most likely have ripples in other areas that you may not know anything about. These other areas may not seem applicable to you now, but they could become very applicable should unknown problems arise. Knowing more about other things can help to prevent those unknown problems.

So what do I suggest? Well, there are certain skills that I think everyone should have (some may depend on gender, I don't think guys should necessarily know how to put on makeup). Now, you don't necessarily have to be a pro at these skills, you just need to know enough to get by. For a guy, these might be things like tying a tie, building a fire, fixing a sink, changing a flat tire, etc. You might stumble through these things with the same level of competence as a monkey trying to land a 747, but at the end of the day all that counts is that you get the job done (by the way, someone should throw a monkey into a 747 simulator and see what happens).

Then there are things that you may not need to be good at, but it might be advantageous to have a fair amount of competence. These things could be related to your job, like if you are in sales then it might help to know some things about the science or engineering behind the products you are selling. Likewise, if you are in the engineering department, then it could help to know about the finance and politics that go into what determines your system specifications. These skills also may not have to be related to your job, they could just be random things that you are passionate about. This can be a good idea if you chose a career that didn't really suit your passion, because it will give you a chance to have some fun but also make some money.

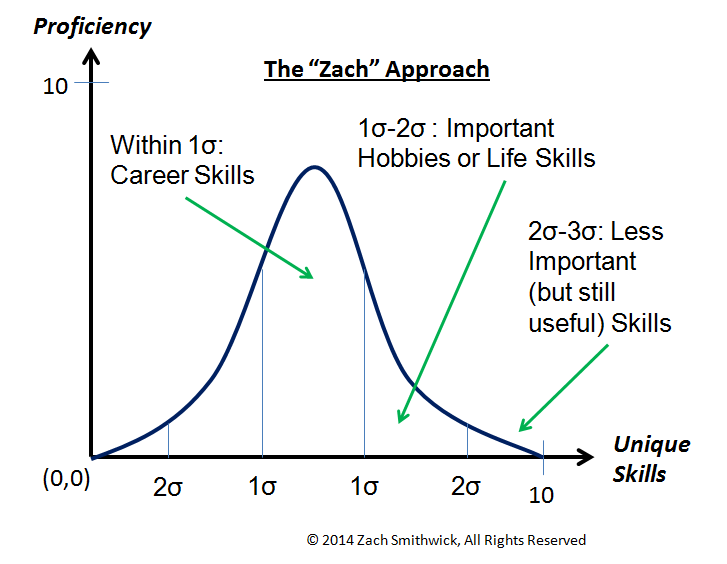
With these things considered, my suggestion would be to employ a sort of Gaussian Distribution or "bell curve" approach to the proficiency/skills graph. It doesn't quite keep with the analogy, but bear with me. If you don't know what a Gaussian (or Normal) Distribution is, then you should look it up because it comes up in a ton of different areas. If you don't wanna look it up, then here is a quick and dirty Normal Distribution lesson: it basically implies that the probability that something happens is centered around a certain value, and then tapers off the further away you get from that value. So let's say you play golf and you are pretty good, then you might say you hit your driver about 300 yards. Now, does every one of your drives go exactly 300 yards? Probably not, unless you are a robot. More than likely, most would fall between maybe 290 and 310 yards, with maybe a few landing shorter than 290 and farther than 310, and even fewer landing shorter than say 250 and longer than 350 (if any). So the point of getting better at golf, and other sports, is reducing your standard deviation, or basically how "off" your bad shots are.

What does this mean in terms of choosing what to concentrate on in life? Well, treat the skills you need for your job as the center of your bell curve. These are the things you need to be the best at, because that will give you the money you need to make everything else happen. Then come the skills that are one standard deviation away. These are things like hobbies you are passionate about or continuing education that doesn't necessarily relate to your job. It can also apply to skills needed for parenting; you don't need to be the perfect parent, but you do need to put a fair amount of effort into it. Then come the things that are two standard deviations away. These are things you really don't have to excel at in any way, you just need to know enough to get by. The good thing about this model is that it allows for a great many things to lie within the realm of possibility, which is more realistic than say 5 things that you can be good at.

It won't be as optimal as having only 55% of your talent going toward 55% of your goals (per the geometrical analogy), but it does give you the ability to do all the things that really matter, and maybe more.

Now it should be noted that this will of course vary according to the individual. Memory will also play a big role. If it takes you a few hours to learn a certain skill and then you never forget it, then it won't consume very much of your life. Likewise if you learn a skill that becomes part of your normal routine, then you can get decently good at it without a major time/effort commitment.

A good example of this would be tying a tie. I, for one, rarely wear ties, so whenever I do I sort of have to re-learn it. This is made pretty easy these days since I can just look up a YouTube video of how to do it. It might take a few more minutes than it needs to, but since I don't do it very often it doesn't take too much out of my life. It would definitely be one of my "3σ skills." Now, on the other hand, if you have to tie a tie on a daily basis, then you will probably get pretty good at it without too much extra time out of your life. Thus, it could be one of your "1σ-2σ Skills" without too much headache.

So next time you are vegging on the couch, stop and think about how you are using your abilities. Are you spending all your "one standard deviation time (or 1σ for short)" to good uses? If so, then you can afford a little vegging as part of your 2σ time, but if not, then you might should get up and spend some time doing things that you are really passionate about!